Task6.神经网络基础-白红宇

Task6.神经网络基础

阅读量：5024 次

发布时间：2019-06-12

本文共 9488 字，大约阅读时间需要 31 分钟。

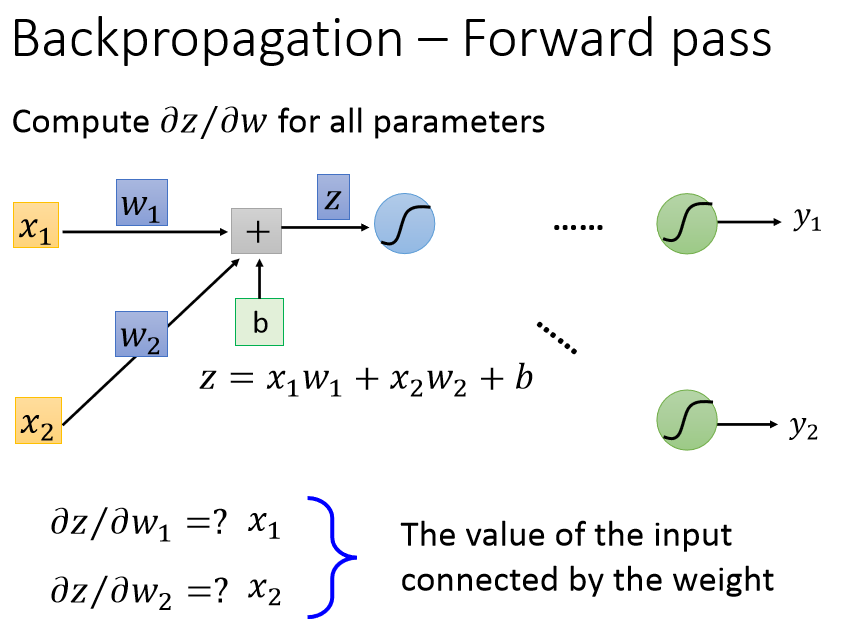
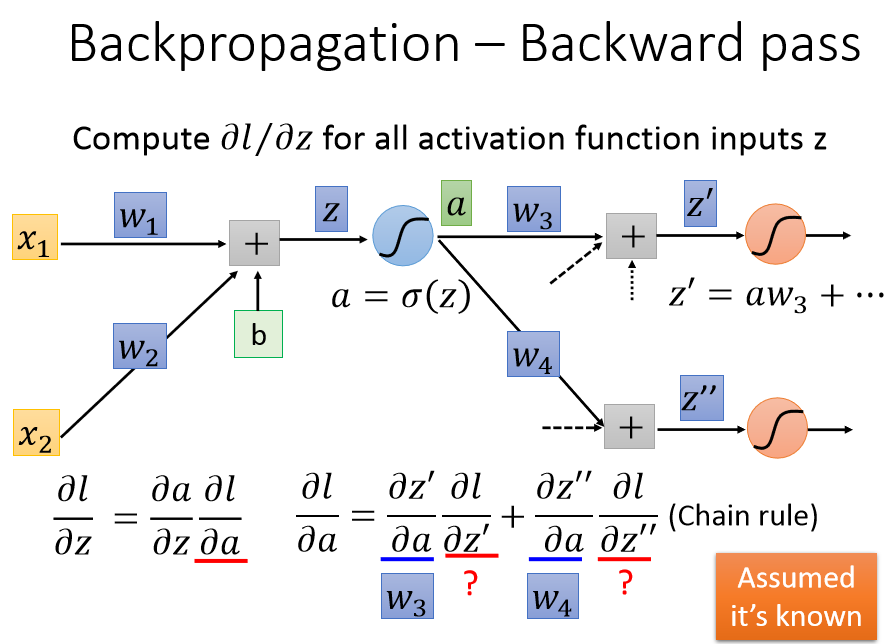
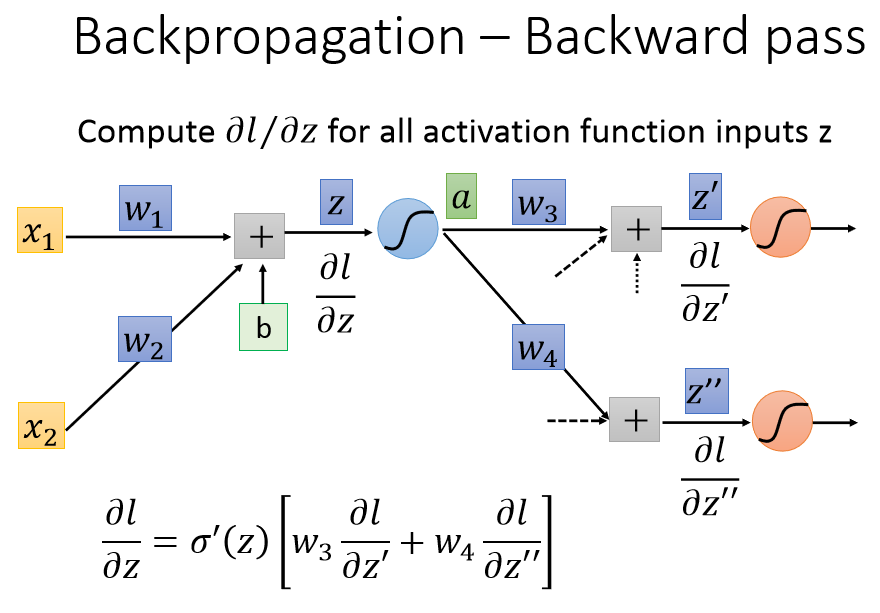
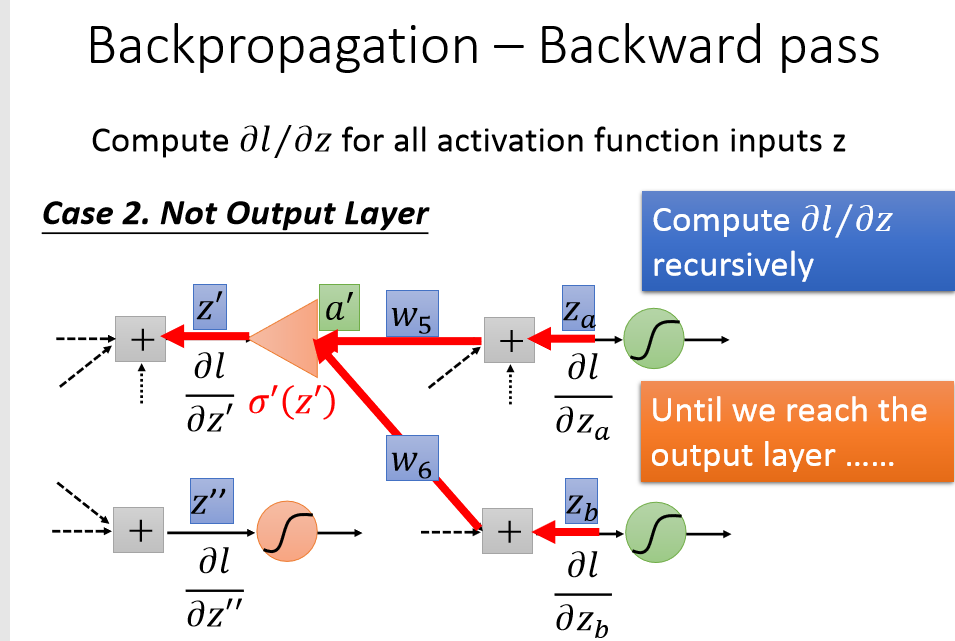
BP:

正向计算loss,反向传播梯度。

计算梯度时，从输出端开始，前一层的梯度等于activation' *（与之相连的后一层的神经元梯度乘上权重的和）。

1 import torch 2 from torch import nn 3 from torch.autograd import Variable 4  5 x_data = [1.0, 2.0, 3.0] 6 y_data = [2.0, 4.0, 6.0] 7  8 # Any random value 9 w = Variable(torch.Tensor([1.0]), requires_grad=True)10 11 # forward pass12 def forward(x):13     return x*w14 15 # Before training16 print("predict (before training)", 4, forward(4))17 18 def loss(x, y):19     y_pred = forward(x)20     return (y_pred-y)*(y_pred-y)21 22 # Training: forward, backward and update weight23 # Training loop24 for epoch in range(10):25     for x, y in zip(x_data, y_data):26         l = loss(x, y)27         l.backward()28         print("\t grad:", x, y, w.grad.data[0])29         w.data = w.data - 0.01 * w.grad.data30         # Manually zero the gradients after running the backward pass and update w31         w.grad.data.zero_()32     print("progress:", epoch, l.data[0])

几种常见的激活函数

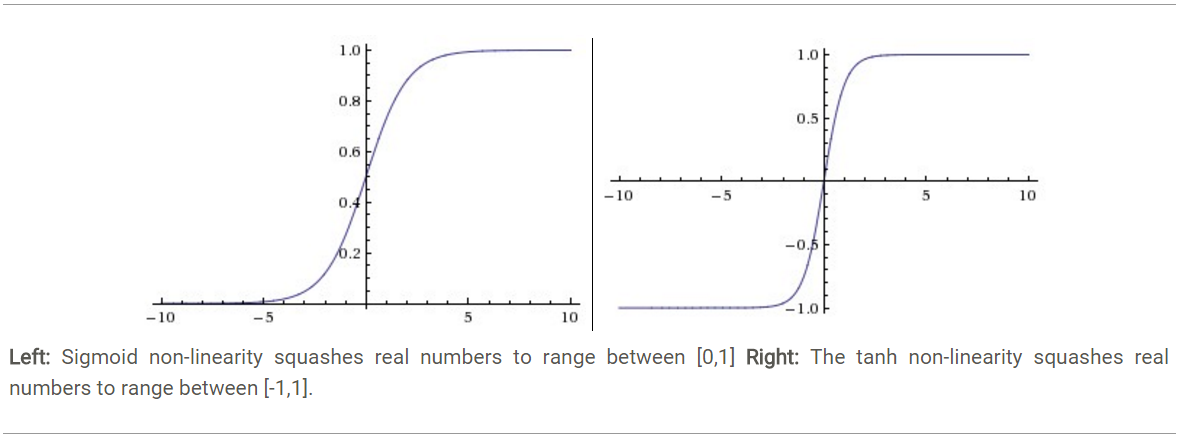
Sigmoid. Sigmoid(也叫逻辑激活函数) 非线性激活函数的形式是，其图形如上图左所示。之前我们说过，sigmoid函数输入一个实值的数，然后将其压缩到0~1的范围内。特别地，大的负数被映射成0，大的正数被映射成1。sigmoid function在历史上流行过一段时间因为它能够很好的表达“激活”的意思，未激活就是0，完全饱和的激活则是1。而现在sigmoid已经不怎么常用了，主要是因为它有两个缺点:

Sigmoids saturate and kill gradients. Sigmoid容易饱和，并且当输入非常大或者非常小的时候，神经元的梯度就接近于0了，从图中可以看出梯度的趋势。这就使得我们在反向传播算法中反向传播接近于0的梯度，导致最终权重基本没什么更新，我们就无法递归地学习到输入数据了。另外，你需要尤其注意参数的初始值来尽量避免saturation的情况。如果你的初始值很大的话，大部分神经元可能都会处在saturation的状态而把gradient kill掉，这会导致网络变的很难学习。

Sigmoid outputs are not zero-centered. Sigmoid 的输出不是0均值的，这是我们不希望的，因为这会导致后层的神经元的输入是非0均值的信号，这会对梯度产生影响：假设后层神经元的输入都为正(e.g. x>0 elementwise in ),那么对w求局部梯度则都为正，这样在反向传播的过程中w要么都往正方向更新，要么都往负方向更新，导致有一种捆绑的效果，使得收敛缓慢。

当然了，如果你是按batch去训练，那么每个batch可能得到不同的符号（正或负），那么相加一下这个问题还是可以缓解。因此，非0均值这个问题虽然会产生一些不好的影响，不过跟上面提到的 kill gradients 问题相比还是要好很多的。

Tanh. Tanh和Sigmoid是有异曲同工之妙的，它的图形如上图右所示，不同的是它把实值得输入压缩到-1~1的范围，因此它基本是0均值的，也就解决了上述Sigmoid缺点中的第二个，所以实际中tanh会比sigmoid更常用。但是它还是存在梯度饱和的问题。Tanh是sigmoid的变形：。

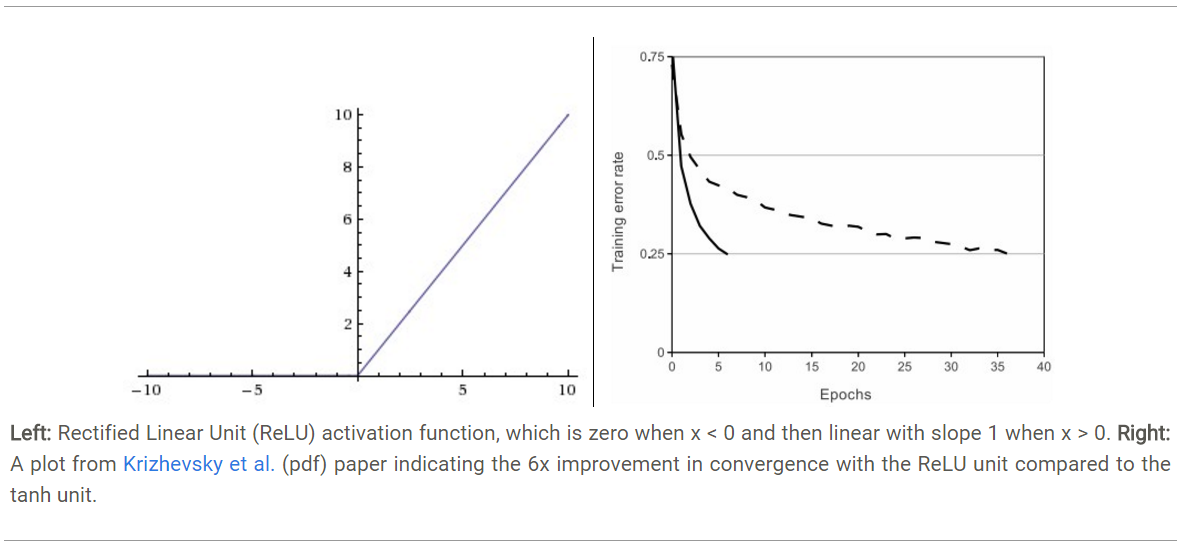
ReLU. 近年来，ReLU 变的越来越受欢迎。它的数学表达式是： f(x)=max(0,x)。很显然，从上图左可以看出，输入信号

<0时，输出为0，>0时，输出等于输入。ReLU的优缺点如下：

优点1：Krizhevsky et al. 发现使用 ReLU 得到的SGD的收敛速度会比 sigmoid/tanh 快很多(如上图右)。有人说这是因为它是linear，而且梯度不会饱和

优点2：相比于 sigmoid/tanh需要计算指数等，计算复杂度高，ReLU 只需要一个阈值就可以得到激活值。

缺点1： ReLU在训练的时候很”脆弱”，一不小心有可能导致神经元”坏死”。举个例子：由于ReLU在x<0时梯度为0，这样就导致负的梯度在这个ReLU被置零，而且这个神经元有可能再也不会被任何数据激活。如果这个情况发生了，那么这个神经元之后的梯度就永远是0了，也就是ReLU神经元坏死了，不再对任何数据有所响应。实际操作中，如果你的learning rate 很大，那么很有可能你网络中的40%的神经元都坏死了。当然，如果你设置了一个合适的较小的learning rate，这个问题发生的情况其实也不会太频繁。

Leaky ReLU. Leaky ReLUs 就是用来解决ReLU坏死的问题的。和ReLU不同，当x<0时，它的值不再是0，而是一个较小斜率(如0.01等)的函数。也就是说f(x)=1(x<0)(ax)+1(x>=0)(x),其中a是一个很小的常数。这样，既修正了数据分布，又保留了一些负轴的值，使得负轴信息不会全部丢失。关于Leaky ReLU 的效果，众说纷纭，没有清晰的定论。有些人做了实验发现 Leaky ReLU 表现的很好;有些实验则证明并不是这样。

- PReLU. 对于 Leaky ReLU 中的a，通常都是通过先验知识人工赋值的。然而可以观察到，损失函数对a的导数我们是可以求得的，可不可以将它作为一个参数进行训练呢? Kaiming He 2015的论文《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》指出，不仅可以训练，而且效果更好。原文说使用了Parametric ReLU后，最终效果比不用提高了1.03%.

-Randomized Leaky ReLU. Randomized Leaky ReLU 是 leaky ReLU 的random 版本, 其核心思想就是，在训练过程中，a是从一个高斯分布中随机出来的，然后再在测试过程中进行修正。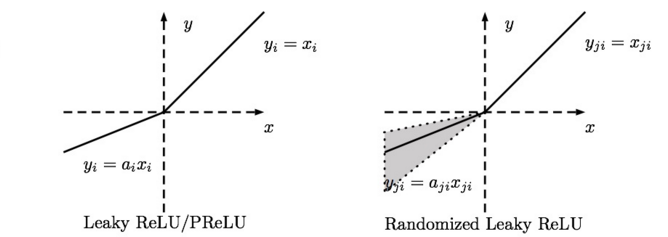

深度学习中的正则化：

1.数据增强：　数据增强通过向训练数据添加转换或扰动来人工增加训练数据集。数据增强技术如水平或垂直翻转图像、裁剪、色彩变换、扩展和旋转通常应用在视觉表象和图像分类中。

2.L1,L2:

L1 和 L2 正则化是最常用的正则化方法。L1 正则化向目标函数添加正则化项，以减少参数的绝对值总和；而 L2 正则化中，添加正则化项的目的在于减少参数平方的总和。根据之前的研究，L1 正则化中的很多参数向量是稀疏向量，因为很多模型导致参数趋近于 0，因此它常用于特征选择设置中。机器学习中最常用的正则化方法是对权重施加 L2 范数约束。

标准正则化代价函数如下：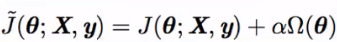

α是惩罚力度，Ω是正则项。

另一种惩罚权重的绝对值总和的方法是 L1 正则化：

L1 正则化在零点不可微，因此权重以趋近于零的常数因子增长。

L1:

L2: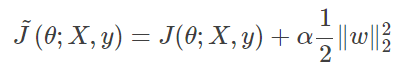

3.Dropout:

Dropout 指暂时丢弃一部分神经元及其连接。随机丢弃神经元可以防止过拟合，同时指数级、高效地连接不同网络架构。神经元被丢弃的概率为 1 p，减少神经元之间的共适应。隐藏层通常以 0.5 的概率丢弃神经元。使用完整网络（每个节点的输出权重为 p）对所有 2^n 个 dropout 神经元的样本平均值进行近似计算。Dropout 显著降低了过拟合，同时通过避免在训练数据上的训练节点提高了算法的学习速度。

4.early stop:

早停法可以限制模型最小化代价函数所需的训练迭代次数。早停法通常用于防止训练中过度表达的模型泛化性能差。如果迭代次数太少，算法容易欠拟合（方差较小，偏差较大），而迭代次数太多，算法容易过拟合（方差较大，偏差较小）。早停法通过确定迭代次数解决这个问题，不需要对特定值进行手动设置。

深度模型中的优化

1.自适应学习率算法

1.1梯度下降

　　梯度下降可以理解为一个人从山顶下山，沿着哪条路径走最快，当然是沿着最陡峭的路径走，就是梯度方向。

1.2AdaGrad

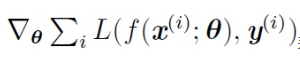
表示第i个参数的梯度，对于经典的SGD优化方法，参数θth的更新为：

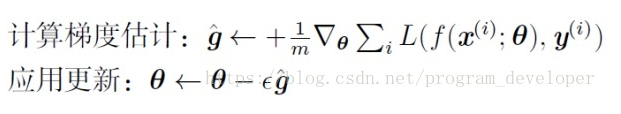
AdaGrad算法表示为：

其中，r为梯度累积变量，r的初始值为0。ε为全局学习率，需要自己设置。δ为小常数，为了数值稳定大约设置为10 -7

AdaGrad算法分析

（1）从AdaGrad算法中可以看出，随着算法不断迭代，r会越来越大，整体的学习率会越来越小。所以，一般来说AdaGrad算法一开始是激励收敛，到了后面就慢慢变成惩罚收敛，速度越来越慢。

（2）在SGD中，随着梯度的增大，我们的学习步长应该是增大的。但是在AdaGrad中，随着梯度g的增大，我们的r也在逐渐的增大，且在梯度更新时r在分母上，也就是整个学习率是减少的，这是为什么呢？

这是因为随着更新次数的增大，我们希望学习率越来越慢。因为我们认为在学习率的最初阶段，我们距离损失函数最优解还很远，随着更新次数的增加，越来越接近最优解，所以学习率也随之变慢。

（3）经验上已经发现，对于训练深度神经网络模型而言，从训练开始时积累梯度平方会导致有效学习率过早和过量的减小。AdaGrade在某些深度学习模型上效果不错，但不是全部。

　　1.3Momentum

SGD方法的一个缺点是，其更新方向完全依赖于当前的batch，因而其更新十分不稳定。解决这一问题的一个简单的做法便是引入momentum。

momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力：

Δxt=ρΔxt−1−ηgt

其中，

　　1.4RMSProp　　

RMSProp算法的全称叫 Root Mean Square Prop，是Geoffrey E. Hinton在Coursera课程中提出的一种优化算法，在上面的Momentum优化算法中，虽然初步解决了优化中摆动幅度大的问题。所谓的摆动幅度就是在优化中经过更新之后参数的变化范围，如下图所示，蓝色的为Momentum优化算法所走的路线，绿色的为RMSProp优化算法所走的路线。

为了进一步优化损失函数在更新中存在摆动幅度过大的问题，并且进一步加快函数的收敛速度，RMSProp算法对权重 W 和偏置 b 的梯度使用了微分平方加权平均数。

其中，假设在第 t 轮迭代过程中，各个公式如下所示：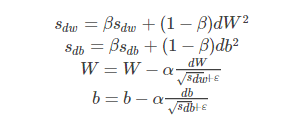

算法的主要思想就用上面的公式表达完毕了。在上面的公式中sdw和sdb分别是损失函数在前t−1t−1轮迭代过程中累积的梯度梯度动量，β 是梯度累积的一个指数。所不同的是，RMSProp算法对梯度计算了微分平方加权平均数。这种做法有利于消除了摆动幅度大的方向，用来修正摆动幅度，使得各个维度的摆动幅度都较小。另一方面也使得网络函数收敛更快。（比如当 dW 或者 db 中有一个值比较大的时候，那么我们在更新权重或者偏置的时候除以它之前累积的梯度的平方根，这样就可以使得更新幅度变小）。为了防止分母为零，使用了一个很小的数值 ϵϵ 来进行平滑，一般取值为 10−8。

　　1.5Adam

有了上面两种优化算法，一种可以使用类似于物理中的动量来累积梯度，另一种可以使得收敛速度更快同时使得波动的幅度更小。那么讲两种算法结合起来所取得的表现一定会更好。Adam（Adaptive Moment Estimation）算法是将Momentum算法和RMSProp算法结合起来使用的一种算法，我们所使用的参数基本和上面讲的一致，在训练的最开始我们需要初始化梯度的累积量和平方累积量。

假设在训练的第 t 轮训练中，我们首先可以计算得到Momentum和RMSProp的参数更新：

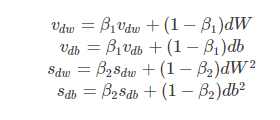
由于移动指数平均在迭代开始的初期会导致和开始的值有较大的差异，所以我们需要对上面求得的几个值做偏差修正。

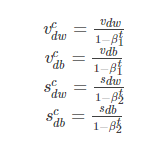
通过上面的公式，我们就可以求得在第 t 轮迭代过程中，参数梯度累积量的修正值，从而接下来就可以根据Momentum和RMSProp算法的结合来对权重和偏置进行更新。

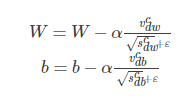
上面的所有步骤就是Momentum算法和RMSProp算法结合起来从而形成Adam算法。在Adam算法中，参数 β1一般取0.9，参数 β2 所对应的就是RMSProp算法中的 β 值，一般我们取0.999，而 ϵ 是一个平滑项，我们一般取值为 10−8，而学习率 α 则需要我们在训练的时候进行微调。

batchnorm

BN的基本思想其实相当直观：因为深层神经网络在做非线性变换前的激活输入值（就是那个x=WU+B，U是输入）随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值WU+B是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因，而BN就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，意思是这样让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

THAT’S IT。其实一句话就是：对于每个隐层神经元，把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的比较标准的正态分布，使得非线性变换函数的输入值落入对输入比较敏感的区域，以此避免梯度消失问题。因为梯度一直都能保持比较大的状态，所以很明显对神经网络的参数调整效率比较高，就是变动大，就是说向损失函数最优值迈动的步子大，也就是说收敛地快。BN说到底就是这么个机制，方法很简单，道理很深刻。

FastText

原理：

fastText 方法包含三部分：模型架构、层次 Softmax 和 N-gram 特征。

fastText 模型输入一个词的序列（一段文本或者一句话)，输出这个词序列属于不同类别的概率。

序列中的词和词组组成特征向量，特征向量通过线性变换映射到中间层，中间层再映射到标签。

fastText 在预测标签时使用了非线性激活函数，但在中间层不使用非线性激活函数。

fastText 模型架构和 Word2Vec 中的 CBOW 模型很类似。不同之处在于，fastText 预测标签，而 CBOW 模型预测中间词。

第一部分：fastText的模型架构类似于CBOW，两种模型都是基于Hierarchical Softmax，都是三层架构：输入层、隐藏层、输出层。

CBOW模型又基于N-gram模型和BOW模型，此模型将W(t−N+1)……W(t−1)W(t−N+1)……W(t−1)作为输入，去预测W(t)

fastText的模型则是将整个文本作为特征去预测文本的类别。

第二部分：层次之间的映射

将输入层中的词和词组构成特征向量，再将特征向量通过线性变换映射到隐藏层，隐藏层通过求解最大似然函数，然后根据每个类别的权重和模型参数构建Huffman树，将Huffman树作为输出。

具体的数学求解过程可参考博客：

第三部分：fastText的N-gram特征

常用的特征是词袋模型（将输入数据转化为对应的Bow形式）。但词袋模型不能考虑词之间的顺序，因此 fastText 还加入了 N-gram 特征。

“我爱她” 这句话中的词袋模型特征是 “我”，“爱”, “她”。这些特征和句子 “她爱我” 的特征是一样的。

如果加入 2-Ngram，第一句话的特征还有 “我-爱” 和 “爱-她”，这两句话 “我爱她” 和 “她爱我” 就能区别开来了。当然，为了提高效率，我们需要过滤掉低频的 N-gram。

在fastText 中一个低维度向量与每个单词都相关。隐藏表征在不同类别所有分类器中进行共享，使得文本信息在不同类别中能够共同使用。这类表征被称为词袋（bag of words）（此处忽视词序）。在 fastText中也使用向量表征单词 n-gram来将局部词序考虑在内，这对很多文本分类问题来说十分重要。

举例来说：fastText能够学会“男孩”、“女孩”、“男人”、“女人”指代的是特定的性别，并且能够将这些数值存在相关文档中。然后，当某个程序在提出一个用户请求（假设是“我女友现在在儿？”），它能够马上在fastText生成的文档中进行查找并且理解用户想要问的是有关女性的问题。

FastText= word2vec中 cbow + h-softmax的灵活使用

灵活体现在两个方面：

模型的输出层：word2vec的输出层，对应的是每一个term，计算某term的概率最大；而fasttext的输出层对应的是

分类的label。不过不管输出层对应的是什么内容，起对应的vector都不会被保留和使用；

模型的输入层：word2vec的输入层，是 context window 内的term；而fasttext 对应的整个sentence的内容，包括term，也包括 n-gram的内容；

两者本质的不同，体现在 h-softmax的使用。

Word2vec的目的是得到词向量，该词向量最终是在输入层得到，输出层对应的 h-softmax 也会生成一系列的向量，但最终都被抛弃，不会使用。

fasttext则充分利用了h-softmax的分类功能，遍历分类树的所有叶节点，找到概率最大的label（一个或者N个）。

用fasttext进行分类：

安装fastText

$ git clone https://github.com/facebookresearch/fastText.git$ cd fastText$ pip install .

(可能会报错，缺少pybind11,pip3 install pybind11)

1 import jieba 2  3 inFile = 'data/data.txt' 4 outFile = 'data/train.txt' 5 f = open(inFile,'r',encoding='utf8') 6 writer = open(outFile,'w',encoding='utf8') 7 for line in f.readlines():    8     splitor = line.split() 9     10     text = jieba.cut_for_search(splitor[0])11     text = ' '.join(text) + " " + splitor[1] + '\n'12     writer.writelines(text)13 f.close()14 writer.close()

line

'北京大学\t__label__college\n'

splitor

['北京大学', '__label__college']

1 import logging 2 import fastText 3 import jieba 4 # help(fastText.FastText) 5 # exit() 6 input="清华大学" 7   8 text = jieba.cut_for_search(input) 9 text = " ".join(text)10  11 # logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)12  13 classifier = fastText.train_supervised("data/trained.txt",epoch=10,ws=2 , lr=0.5, wordNgrams=1, dim=1000,label=u"__label__",loss=u'softmax')14  15 classifier.save_model("model/classify.model")16  17 result = classifier.predict(text)18  19 print("预测词：" + input + "\n")20  21 print("预测结果：")22 print( result)